Fibonacci analyzoval posloupnost čísel, začínající čísly 0 a 1, v níž se každé následné číslo vypočítá součtem dvou čísel předchozích. Fibonacci objevil, že tuto posloupnost charakterizuje zajímavý rys – čím jsou čísla v posloupnosti vyšší, tím víc se podíl každých dvou po sobě jsoucích čísel blíží nekonečnému číslu 1,6182[…].
Bylo objeveno, že číslo 1,6182[…], zvané fí (Φ nebo φ), má velký význam v různých oblastech vědy, např. v biologii, architektuře a jiných, a proto se díky svým zvláštnostem nazývá také zlaté číslo nebo zlatý poměr.
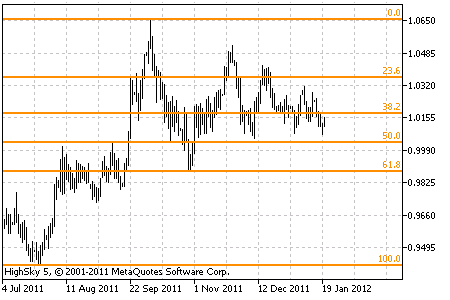
Zlaté číslo se používá i na finančních trzích, a sice v prognostických a rozhodovacích metodách. Jiným klíčovým číslem je 0,6182, které vznikne vydělením čísla z Fibonacciho posloupnosti číslem následným, nebo odečtením jedničky od zlatého čísla.
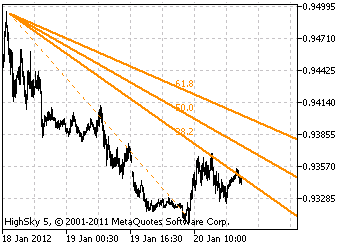
Mezi nástroje založené na teoriích, z nichž vycházejí Fibonacciho čísla, patří: Fibonacciho vějíře, oblouky, časová pásma, obraty, kanály a expanze, z nichž nejrozšířenější jsou Fibonacciho obraty.
Od roku 2008 se věnujeme široké škále témat s důrazem na finance, investování a podnikání. Články píšeme srozumitelně, abychom každému čtenáři pomohli objasnit i ta nejsložitější témata. Autor vystudoval ekonomii a management.
